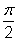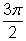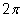Compound Functions
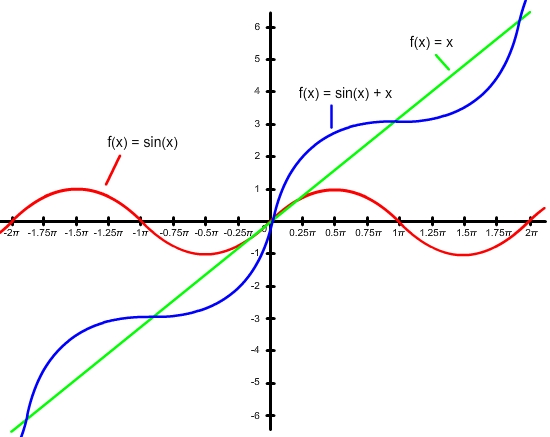
Another type of function that can be graphed is called a compound function. Compound functions are sums or products of trigonometric functions such as f(x) = sin(x) + x or 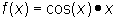 .
.
If you want to graph compound functions, you can graph each of the parts separately and then add or multiply them together. Remember that subtraction problems can always be rewritten as addition problems. For example: f(x) = cos(x) - x can be rewritten as f(x) = cos(x) + (-x).
Start with f(x) = sin(x) + x. You can look at the following table values to see what happens when these two functions are added together.
| x | 0 |
|
|
|
|
| sin(x) | 0 | 1 | 0 | -1 | 0 |
| sin(x) + x | 0 + 0 = 0 | 1.57 + 1 = 2.57 | 3.14 + 0 = 3.14 | 4.71 - 1 = 3.71 | 6.28 + 0 = 6.28 |
(Remember that
 )
) Now we can graph this new information: