Phase Shift (continued)
The following problem shows how the definition of phase shift works:
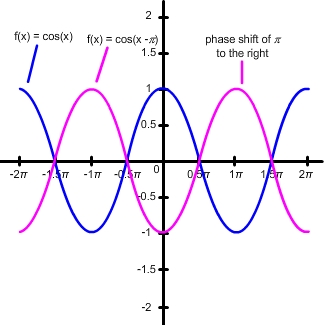
Graph  . What is the phase shift of this function and in which direction will you move the graph?
. What is the phase shift of this function and in which direction will you move the graph?
In this problem, c =  and k = 1. The phase shift is
and k = 1. The phase shift is 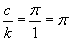 .
.
Since c > 0, the graph will shift to the right of the basic function.
Look at another example of how a phase shift will change the graph of a trigonometric function.
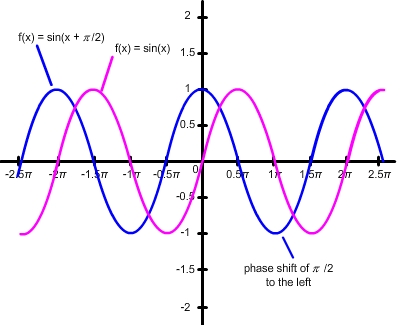
Graph 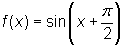 . What is the phase shift of this function and in which direction will you move the graph?
. What is the phase shift of this function and in which direction will you move the graph?
Sometimes it is easy to confuse the sign for c when there is an addition sign within the parenthesis. The best way to avoid making a mistake is to rewrite the equation to reflect the general equation given in your definition. Therefore, rewrite 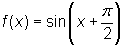 as
as 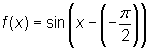 . Now it is easier to see that
. Now it is easier to see that 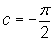 .
.
Since k = 1 and 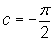 , the phase shift,
, the phase shift,  , is
, is 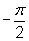 . This graph will shift to the left of the basic function since c < 0.
. This graph will shift to the left of the basic function since c < 0.