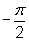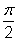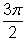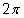Transformations of Trigonometric Functions, Page 2

Amplitude

The first topic that needs to be discussed is the amplitude of a function. The amplitude is the value of half the distance between the minimum and maximum values of the range of a periodic function. 

For f(x) = Asin(x) and f(x) = Acos(x), the amplitude is defined as the absolute value of A, written as |A|. Remember that absolute value is a measure of distance; therefore, it can never be negative. For example: |3| = 3 and |-3| = 3.

Another way to state the definition of amplitude is to write the equation: 



The following diagram illustrates the amplitude of a trigonometric function: 



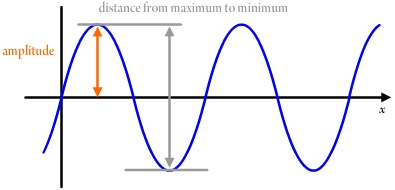
The following is an example that shows what happens to the graph of a trigonometric function when you change the amplitude.

For f(x) = 3sin(x), A = 3, therefore, the amplitude is |3| = 3.

You need to look at the graphs of f(x) = 3sin(x) and f(x) = sin(x) to see how they compare and note how the value of A changes the graph of f(x) = sin(x).

You start by building a table of the values:

x			-		0
sin(x)	0	1	0	-1	0	1	0	-1	0
3sin(x)	0	3	0	-3	0	3	0	-3	0

Now graph the two functions together so you can compare them: 



The dotted lines represent the maximum and minimum values of f(x) = 3sin(x). The maximum value is 3 and the minimum value is -3. Given the equation for amplitude:



You can now see how the amplitude equation works. You should also notice that this amplitude value makes the graph three times taller than our original function f(x) = sin(x).

Please note: The tangent function has no amplitude because it has no minimum or maximum values.

Next Previous 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

© 2007 Aventa Learning. All rights reserved.